From the information provided, we have a total of 103 coins. We do not know the number of dimes and quarters but its all a total of $15.25. This can be rewritten as 1525 cents.
Note also that;
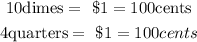
For the total number of coins, we would have;
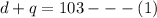
For the total amount of money available, we would have;
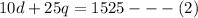
We would now take equation (1). Make d the subject of the equation and we'll have;
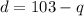
Substitute for d into equation (2);

We can now collect like terms, and we'll have;
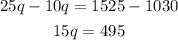
We next divide both sides by 15;
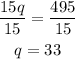
This means we have 33 quarters. We can now substitute for the value of q into equation (1);

ANSWER:
We now have,
70 dimes and 33 quarters