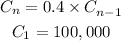Since each day, the amount of candy that Augustus will give away is 60% of the actual amount of candy, the amount of candy that has on day n depends on the amount of candy remaining from the day n-1. Let C_n be the amount of candy remaining on day n.
Since 60% of the candy from the day n-1 will be given away, then only 40% from the candy of the day n-1 will remain on day n. Then:

Since the amount of candy on day 1 is 100,000, then the recursive formula is:
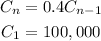
After n-1 days, the initial amount of candies gets multiplied by a factor of 0.4 n-1 times. Then, the explicit formula for the amount of candies that remain on day n (after n-1 days) is:

Therefore, the answers are:
Explicit formula:
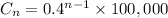
Recursive formula: