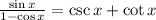We want to simplify the following expression
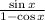
We can start by multiplying both numerator and denominator by the conjugate of the denominator:
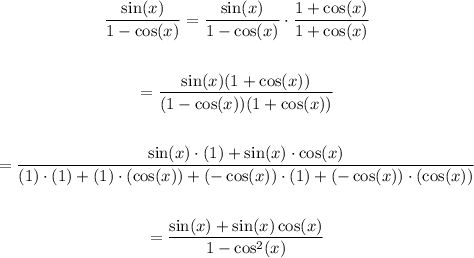
Then, using the identity
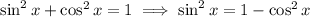
We can rewrite our expression as
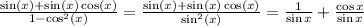
By definition of cosecant and cotangent, our expression can be written as
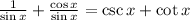
and this is our answer.