We will proceed as follows:
a)

From this, we can see that the x-intercepts are located at (-5, 0) & (5, 0).
The y-intercepts are located at (0,4) & (0, -4).
The domain is [-5, 5] and their range is [-4, 4]
b)
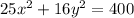
From this, we can see that the x-intercepts are located at (-4, 0) & (4, 0).
The y-intercepts are located at (0, 5) & (0, -5).
The domain is [-4, 4], and the range [-5, 5].
***
For ellipsis, we find their x & y-intercepts as follows:
*Since they are written in the form:

The value a that accompanies x will give as a solution the y-component of the y-intercept, and the b value that accompanies the y-component gives the x-component of the x-intercept.
*The domain is given by greatest and lowest x-values [The extremes of the shape] and the range is given by the greatest and lowest y-values.