Question

A boat speeds at 30 m/s crossing a river that is 200 m wide. The river flows from north to south at 10 m/s and the boat leaves the west shore traveling at 25 S of E. a) what is the boat’s displacement when it reaches the other side? b) what is boat’s velocity seen from stationary helicopter above?c)at what angle would one have to face boat without any intervention so it ends up directly across the river?

Answer 1

a) First, consider that the horizontal component of the initial velocity is given by:

`v_(ox)=30(m)/(s)\cdot\cos (25)=27.19(m)/(s)`

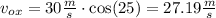
The horizontal component of the velocity is constant in all the trajectory of the boat, then, the time it takes to cross the river can be calulated as follow:

`t=(x)/(v_(ox))=(200m)/(27.19(m)/(s))=7.35s`

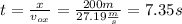
Next, take into account that the vertical distance traveled by the boat, in the previous time, depends on the speed of the flow of the river and the vertical component of the velocity of the boat, as follow:

`\begin{gathered} y=(v_(oy)+10(m)/(s))(7.35s)=(30(m)/(s)\cdot\sin (25)+10(m)/(s))(7.35) \\ y=166.68m \end{gathered}`

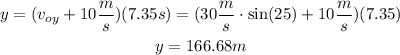
Now, use the Pythagorean theorem to find the displacement, as follow:

`d=\sqrt[]{x^2+y^2}=\sqrt[]{(200m)^2+(166.68m)^2}=260.35m`

Hence, the displacement was approximately 260.35m

b) The boat's velocity can be obtained by using the following velocity vector diagram:

where vo is the speed of the boat crossing the river vo = 30 m/s.

Use the law of cosines to find the speed of the boat seen by a stationary helicopter:

`\begin{gathered} v^2=30^2+10^2-2(30)(10)\cos 115 \\ v=35.40(m)/(s) \end{gathered}`

Hence, the speed is 35.40 m/s

c) If we need the boat ends up directly acroos the river, it is necessary that the vertical component of its velocity is opposite to thespeed of the flow of the river.

Then, you have:

`\begin{gathered} v_(oy)=v_o\sin \theta=-10 \\ \theta=\sin ^(-1)(-(10)/(v_o)) \\ \theta=\sin ^(-1)(-(10)/(30)) \\ \theta=-19.47 \end{gathered}`

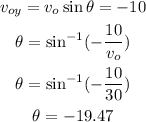
Hence, the angle would be 19.47 degrees N of E