Question

6. Find the area of the composite figure.7 in.6 in3 in.51 inches squared60 inches squared45 inches squarednone of the given answersOther:

Answer 1

To obtain the area of the composite figure, the following steps are necessary:

Step 1: Recall the formulas for the area of a rectangle and a triangle (since they both make up the composite figure), as given below:

`\begin{gathered} A_(rec\tan gle)=length\text{ }* width \\ A_(triangle)=(1)/(2)* base* height \end{gathered}`

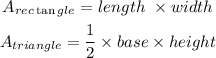
Step 2: Compute the areas of the rectangle and triangle using the formulas above

`\begin{gathered} A_(rec\tan gle)=length\text{ }* width \\ \Rightarrow A_(rec\tan gle)=7\text{ }*6=42 \\ A_(triangle)=(1)/(2)* base* height \\ \Rightarrow A_(triangle)=(1)/(2)*3*6=(18)/(2)=9 \end{gathered}`

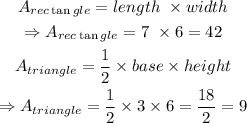
Step 3: Add the two areas together, as follows:

`A_(composite)=A_(rec\tan gle)+A_(triangle)`

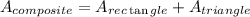
Thus:

`\begin{gathered} A_(composite)=42+9=51 \\ \Rightarrow A_(composite)=51in^2 \end{gathered}`

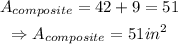
Therefore, the area of the composite figure is 51 inches squared (option A)