Question

15. The table below shows the population of California from 2010 to 2019.YearPopulation (millions)201037.32011 37.6201238.0201338.3201438.6201538.9201639.2201739.4201839.5201939.5(a) Use a graphing calculator to build a logistic regression model that best fits this data, letting t=0 in 2010. Round each coefficient to two decimal places.Pt= (b) What does this model predict that the population of California will be in 2025? Round your answer to one decimal place. million people(c) When does this model predict that California's population will reach 40 million? Give your answer as a calendar year (ex: 2010).During the year

Answer 1

Using a graphing calculator, we obtain the following regression model.

Thus, the regression model is:

`\begin{gathered} P(t)=0.261212t+37.4545 \\ P(t)=0.26t+37.45 \end{gathered}`

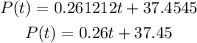
For part b, find the value of x by subtracting 2025 by 2010. Thus, the value of t is 15. Substitute 15 for t in the obtained equation in part a and then solve for P(t).

`\begin{gathered} P(t)=0.26t+37.45 \\ =0.26(15)+37.45 \\ =3.9+37.45 \\ =41.35 \end{gathered}`

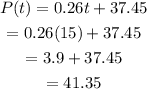
Thus, there is approximately 41.4 million people on 2025.

For part c, substitute 40 for P(t) in the obtained equation in part a and then solve for t.

`\begin{gathered} P(t)=0.26t+37.45 \\ 40=0.26t+37.45 \\ 40-37.45=0.26t \\ 2.55=0.26t \\ t=(2.55)/(0.26) \\ t\approx9.807692308 \\ t\approx10 \end{gathered}`

Add the obtained value of t to 2010. Thus, the population will reach 40 million in 2020.