Answer:
The measure of the sides are;
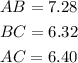
Classifying the triangle by its sides. The triangle is a Scalene triangle
Step-by-step explanation:
We want to find the length of the triangle ABC.
Recall that the distance between two points can be calculated using the formula;
![d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/be685jmxw05hm2tq94m5iuge2xjynn1hfn.png)
Given;

For the given points A, B and C, the distance between the points are;
For side AB;
![\begin{gathered} AB=\sqrt[]{(3-1)^2+(-2-5)^2} \\ AB=\sqrt[]{2^2+(-7)^2} \\ AB=\sqrt[]{4+49} \\ AB=\sqrt[]{53} \\ AB=7.28 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9v0n8pn2pqpdqk4ysg8b2n71iqxiczhvfe.png)
For side BC;
![\begin{gathered} BC=\sqrt[]{(-3-3)^2+(0-(-2))^2} \\ BC=\sqrt[]{(-6)^2+(2)^2} \\ BC=\sqrt[]{36+4} \\ BC=\sqrt[]{40} \\ BC=6.32 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/yi4k5ovc4jxe24artgoemvfpcne36buwpn.png)
For side AC;
![\begin{gathered} AC=\sqrt[]{(-3-1)^2+(0-5)^2} \\ AC=\sqrt[]{(-4)^2+(-5)^2} \\ AC=\sqrt[]{16+25} \\ AC=√(41) \\ AC=6.40 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/n7hm52qintmzo7m6jtkg2jodqj1plo6pbq.png)
So, the measure of the sides are;
From the derived length of the sides of the triangle, classifying the triangle by its sides. The triangle is a Scalene triangle.
Because it has no equal sides.