Step-by-step explanation
Let the number of each type of greeting cards be represented by x and y.
Since there are 6 greeting cards in total; it follows that:

If x greeting card costs $2 each, then the total cost of that type of card = 2x
Also, if y greeting card costs $3 each, then the total cost of that type of card = 3y.
Therefore, if Lola paid $13 for the 6 greeting cards, it follows that:
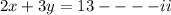
Hence, the system of equations that represent this situation is:
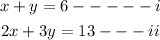
To solve the system of equations, use the elimination method.
Multiply (i) by 3

To solve for y, put x = 5 into equation (i)
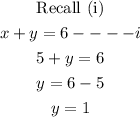
Hence, the solution to the system of equations is x = 5, and y = 1
The interpretation of the solution
x = 5 implies there are 5 greeting cards that cost $2 each.
y = 1 implies there is 1 greeting card that cost $3 each.