Question

A) list the real number roots and it’s multiplicityB) domain and range C) degree : 4 D) equation (show work by solving for “a”)

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write how to get the roots

The roots of the graph can be gotten by picking the x-intercepts. Hence, the real number roots will be:

`-3,-1,1,3`

STEP 2: Explain how to get the multiplicity

To get the multiplicity from a given graph;

If the graph crosses the x-axis and appears almost linear at the intercept, it is a single zero.

If the graph touches the x-axis and bounces off of the axis, it is a zero with even multiplicity.

From the graph give, the roots all have multiplicity of 1.

Therefore, the roots are -3,-1,1,3

The roots all have a multiplicity of 1

STEP 3: Get the domain and range

The domain refers to the set of possible input values, the domain of a graph consists of all the input values shown on the x-axis. The range is the set of possible output values, which are shown on the y-axis.

Therefore the domain will be,

STEP 4: Calculate the degree of the function

The degree of the function is the sum of the multiplicities. The degree of a term is the sum of the exponents of the variables that appear in it, and thus is a non-negative integer. Recall that we have four roots all with a multiplicity of 1.

Therefore, the degree is 4

STEP 5: Get the equation

The equation of a polynomial has a standard form given as:

`\begin{gathered} y=a(x+m)(x+b)(x+c)(x+d) \\ where\text{ m,b,c and d are the zeroes or the roots} \end{gathered}`

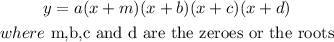
Using the selected point on the graph which is (0,9), we substitute these values into the form above as seen below:

`\begin{gathered} \text{For the given graph,} \\ m=-3,b=-1,c=1,d=3 \\ a=?,x=0,y=9 \end{gathered}`

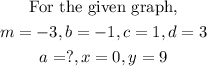
By substitution,

`\begin{gathered} 9=a(0-3)(0-1)(0+1)(0+3) \\ 9=a(-3)(-1)(1)(3) \\ 9=a\cdot9 \\ 9=9a \\ Divide\text{ both sides by 9} \\ (9)/(9)=(9a)/(9) \\ 1=a \\ a=1 \end{gathered}`

Therefore, the equation of the function plotted on the graph will be:

`y=(x+3)(x+1)(x-3)(x-1)`