Question

Create a table of values to represent the equation y = x - 4

Answer 1

Step-by-step explanation:

In order to create a table of points we choose specific values of x and value y =x - 4 for them. This gives us a table of a pair of (x, y) values. This table can then be used to study the equation itself by plotting the table values.

Now let us arbitrarily choose x = -1 , 0 , 1 , 2, 3 and evalute our equation for them.

For x = -1 we have

`y=(-1)-4`
`y=-5`

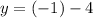
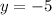
Hence for x = -1 we have y = -5.

For x = 0, we have

`y=0-4`
`y=-4`

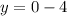
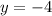
Hence, for x = 0, we have y = -4.

For x = 1 we have

`y=1-4`
`y=-3`

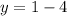
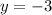
Hence, for x = 1 we have y = -3.

For x = 2, we have

`y=2-4`
`\Rightarrow y=-2`

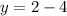
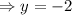
Meaning, for x = 2 we have y = -2.

Finally, for x = 3, we have

`y=3-4`
`\Rightarrow y=-1`

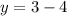
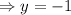
meaning for x = 3 we have y = -1.

So what are the pairs of values we got?

They are given in the following table

x | y

-1 | -5

0 | -4

1 | -3

2 | -2

3 | -1

which is our answer!

Note: we can create as lengthy a table as we want by evaluating the equation y = x - 4 at still more x-values.