Arrange the given data in ascending order.
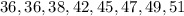
The range is difference between highest and lowest value.
Determine the range for the data.
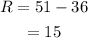
So range is 15.
The lower half of the data is 36,36,38 and 42 and upper half f the data is 45,47,49 and 51.
Determine the Quartile 1 and Quartile 3 for the data.
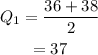
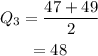
Determine the Inter Quartile range (IQR) for the data.
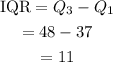
So IQR is 11.
Determine the mean value of the data.
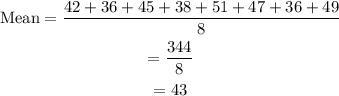
Determine the absolute deviation of the data.
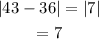
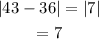
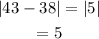
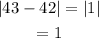
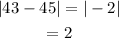
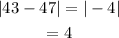
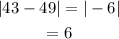
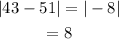
Determine the mean value for the absolute deviation.
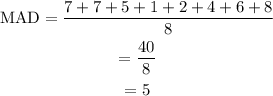
So value of Mean Absolute Deviation (MAD) is 5.