To answer this question, we need to rewrite both equations in the slope-intercept form of the line. To achieve this, we can proceed as follows:
1. We need to isolate the variable y in both equations. In the first equation, we need to subtract 3x from both sides of the equation:
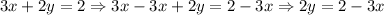
And now, we need to divide both sides by 2 (to isolate the y variable):
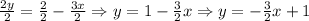
2. We can proceed in a similar way to find the slope-intercept form of the other line:
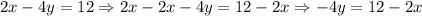
Then, we have:
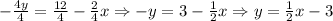
Then, we have both line equations in the slope-intercept form.
Now, to graph both equations, we can use the coordinates of the x- and y-intercepts of both lines:
3. The x-intercept is the point when y = 0. Likewise, the y-intercept is the point when x = 0. We need to evaluate the equation in both cases. Then, we have:
First Line
For y = 0:

Then, we have the first coordinate: (2/3, 0).
For x = 0:
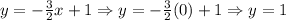
Then, the other coordinate for this point is (0, 1)
To graph this line we can use these two points (0, 1) and (2/3, 0).
Second Line
We can proceed in a similar way to find these two coordinates for the second line:
For y = 0:
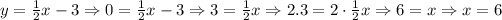
The x-intercept is (6, 0).
For x = 0:
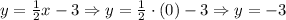
The y-intercept is (0, -3).
To graph this line we can use these two points (0, -3) and (6, 0).
Therefore, the solution for this system of equations is x = 2, y = -2.