Question

If triangle MNP has vertices at M(-5,-7), N(7,-2) and P(2,10) is triangle MNP and isosceles? Provide evidence to support your claim.

Answer 1

Triangle MNP is Isosceles.

Step-by-step explanation:

If triangle MNP has vertices at M(-5,-7), N(7,-2) and P(2,10)

To determine if it is Isosceles or not, we have to find the side lengths using the distance formula.

`Distance=√((x_2-x_1)^2+(y_2-y_1)^2)`

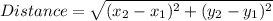
Therefore:

`\begin{gathered} MN=\sqrt[]{(-5-7)^2+(-7-(-2))^2} \\ =\sqrt[]{(-12)^2+(-7+2)^2} \\ =\sqrt[]{(-12)^2+(-5)^2} \\ =\sqrt[]{169} \\ =13\text{ units} \end{gathered}`

Similarly:

`\begin{gathered} MP=\sqrt[]{(-5-2)^2+(-7-10)^2} \\ =\sqrt[]{(-7)^2+(-17)^2} \\ =\sqrt[]{338^{}} \\ =13\sqrt[]{2}\text{ units} \end{gathered}`

Finally:

`\begin{gathered} NP=\sqrt[]{(7-2)^2+(-2-10)^2} \\ =\sqrt[]{(5)^2+(-12)^2} \\ =\sqrt[]{169^{}} \\ =13\text{ units} \end{gathered}`

We see that:

MN=NP=13 Units

Since two sides are equal in length, triangle MNP is Isosceles.