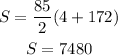Question

Compute the sums below. (Assume that the terms in the first sum are consecutive terms of an arithmetic sequence.) 4 + 6 + 8 + ... + 172 =

Answer 1

`S=7480`

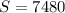
Explanation:

The sum of an arithmetic sequence is represented by the following equation:

`\begin{gathered} S=(n)/(2)(a_1+a_n) \\ \text{where,} \\ a_1\text{= first term} \\ a_n=\text{ nth term of the sequence} \\ n=\text{position of the term} \end{gathered}`

As a first step we need to find the position n for 172 since the common difference is 2:

`\begin{gathered} a_n=a_1+d(n-1) \\ 172=4+2(n-1) \\ \end{gathered}`

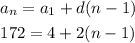
Solve for n.

`\begin{gathered} 172=4+2n-2 \\ 172-2=2n \\ 170=2n \\ n=(170)/(2) \\ n=85 \end{gathered}`

Now, if the first term is 4, the last term is 172 and n=85. The sum of the arithmetic sequence would be:

`\begin{gathered} S=(85)/(2)(4+172) \\ S=7480 \end{gathered}`