Question

I need this practice problem explained I will provide a picture with the answer options

Answer 1

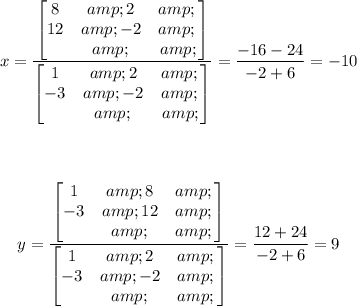
Given the following System of Equations:

`\begin{cases}x+2y=8 \\ -3x-2y=12\end{cases}`

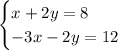
You can solve it with Cramer's Rule. The steps are shown below:

1. By definition, you know that for "x"

`x=(D)/(D_x)=\frac{\begin{bmatrix}{c_1} & {b_1} & {} \\ {c_2_{}_{}_{}} & {b_2} & {} \\ {} & {} & \end{bmatrix}}{\begin{bmatrix}{a1_{}} & {b_1} & {} \\ {a_2_{}} & {b_2} & {} \\ {} & {} & \end{bmatrix}}`

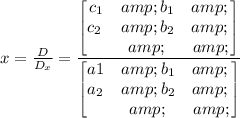
In this case:

`\begin{gathered} c_1=8 \\ c_2=12_{} \\ b_1=2 \\ b_2=-2_{} \\ a_1=1 \\ a_2=-3 \end{gathered}`

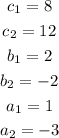
Then, you can substitute values and evaluating, you get that the value of "x" is:

`x=\frac{\begin{bmatrix}{8_{}} & {2_{}} & {} \\ {12_{}} & {-2_{}} & {} \\ {} & {} & \end{bmatrix}}{\begin{bmatrix}{1_{}} & {2_{}} & {} \\ {-3_{}} & {-2_{}} & {} \\ {} & {} & \end{bmatrix}}=((-2)(8)-(2)(12))/((-2)(1)-(2)(-3))=(-16-24)/(-2+6)=-10`

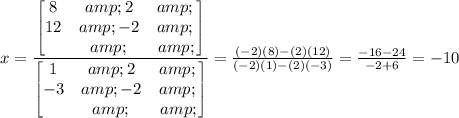
2. By definition, for "y":

`y=(D_y)/(D)=\frac{\begin{bmatrix}{a_1} & {c_1} & {} \\ {a_2} & {c_2} & {} \\ {} & {} & {}\end{bmatrix}}{\begin{bmatrix}{a_1} & {b_1} & {} \\ {a_2} & {b_2} & {} \\ {} & {} & {}\end{bmatrix}}`

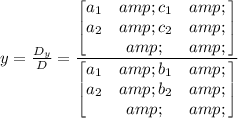
Knowing the values, substitute and evaluate:

`y=\frac{\begin{bmatrix}{1_{}} & {8_{}} & {} \\ {-3_{}} & {12_{}} & {} \\ {} & {} & {}\end{bmatrix}}{\begin{bmatrix}{1_{}} & {2_{}} & {} \\ {-3_{}} & {-2_{}} & {} \\ {} & {} & {}\end{bmatrix}}=((12)(1)-(-3)(8))/((-2)(1)-(-3)(2))=(12+24)/(-2+6)=9`

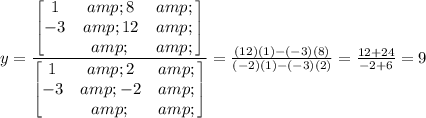
Therefore, the answer is:

`\begin{gathered} x=\frac{\begin{bmatrix}{8_{}} & {2_{}} & {} \\ {12_{}} & {-2_{}} & {} \\ {} & {} & \end{bmatrix}}{\begin{bmatrix}{1_{}} & {2_{}} & {} \\ {-3_{}} & {-2_{}} & {} \\ {} & {} & \end{bmatrix}}=(-16-24)/(-2+6)=-10 \\ \\ \\ y=\frac{\begin{bmatrix}{1_{}} & {8_{}} & {} \\ {-3_{}} & {12_{}} & {} \\ {} & {} & {}\end{bmatrix}}{\begin{bmatrix}{1_{}} & {2_{}} & {} \\ {-3_{}} & {-2_{}} & {} \\ {} & {} & {}\end{bmatrix}}=(12+24)/(-2+6)=9 \end{gathered}`