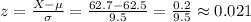In this case, we will use the z-score to compare each student to the distribution corresponding to each career.
a) Evan took a test in Art History and he earned a 74.1.
The scores in Art History have a mean of 70.6 and a standard deviation of 8.9.
We can then calculate the corresponding z-score for this result as:
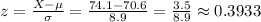
b) Jeff took a test in Social Studies and earned a 62.7.
The scores in Social Studies have a mean of 62.5 and a standard deviation of 9.5.
Then, we can calculate the z-score as: