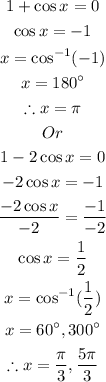Answer:
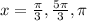
Step-by-step explanation:
Given the below;
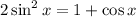
We'll follow the below steps to solve for x;
Step 1: Rewrite using the below trig identity;
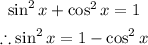
So, we'll have;
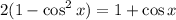
Step 2: Apply the difference of squares formula to the left-hand side of the equation;
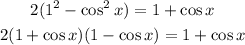
Step 3: Subtract (1 + cos x) from both sides;
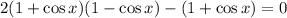
Step 4: Factor out (1 + cos x);
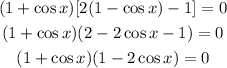
Step 5: Solve for the values of x by equating each term to zero;