Question

Suppose you have to decide which of two jobs you will work: A. Job A: $35,000 for the first year with a $1,500 raise every year thereafter. B. Job B: $30,000 for the first year with a 7% raise every year thereafter. C. Create an equation for each situation. D. Use each equation to complete the table to the right. E. When will job B earn more than Job A? F. Which job would you choose and why?

Answer 1

Job A:

The initial amount is $35 000

The amount of increase for each year is $1500

We can write an equation for this situation

Where x is the number of years

`y_A=35000+1500x`

Job B:

The initial amount is $30 000

The percent of the increase is 7%

Change it to decimal and find the factor of growth

`(7)/(100)=0.07`

The factor of growth = 1 + 0.07 = 1.07, then

The equation is

`y_B=30000(1.07)^x`

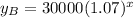
Let us complete the table

`\begin{gathered} x=0 \\ y_A=35000+1500(0)=35000 \\ y_B=30000(1.07)^(0-1)=30000 \end{gathered}`
`\begin{gathered} x=1 \\ y_A=35000+1500(1)=36500 \\ y_B=30000(1.07)^1=32100 \end{gathered}`
`\begin{gathered} x=2 \\ y_A=35000+1500(2)=38000 \\ y_B=30000(1.07)^2=34347 \end{gathered}`
`\begin{gathered} x=3 \\ y_A=35000+1500(3)=39500_{} \\ y_B=30000(1.07)^3=36751.29 \end{gathered}`
`\begin{gathered} x=4 \\ y_A=35000+1500(4)=41000 \\ y_B=30000(1.07)^4=39323.88 \end{gathered}`
`\begin{gathered} x=5 \\ y_A=35000+1500(5)=42500 \\ y_B=30000(1.07)^5=42076.55 \end{gathered}`
`\begin{gathered} x=6 \\ y_A=35000+1500(6)=44000 \\ y_B=30000(1.07)^6=45021.9 \end{gathered}`
`\begin{gathered} x=7 \\ y_A=35000+1500(7)=45500 \\ y_B=30000(1.07)^7=48173.44 \end{gathered}`
`\begin{gathered} x=8 \\ y_A=35000+1500(8)=47000 \\ y_B=30000(1.07)^8=51545.59 \end{gathered}`
`\begin{gathered} x=9 \\ y_A=35000+1500(9)=48500 \\ y_B=30000(1.07)^9=55153.78 \end{gathered}`
`\begin{gathered} x=10 \\ y_A=35000+1500(10)=50000 \\ y_B=30000(1.07)^(10)=59014.54 \end{gathered}`
`\begin{gathered} x=11 \\ y_A=35000+1500(11)=51500 \\ y_B=30000(1.07)^(11)=63145.56 \end{gathered}`

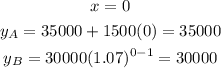
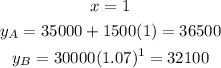
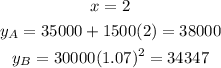
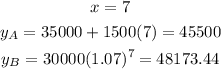
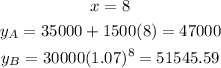
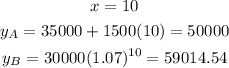
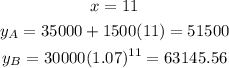
Now let us compare between them

Job A earns more than job B till x = 5, then

Job B will earn more than job A after 5 years (starting from year 6)

Since j