Question

. The slope of the function, g(x) is 5. What is the value of k if g(k) = 3 and g(5) = 2k?

Answer 1

Given that it is a linear function, we know the form:

`g(x)=mx+b`

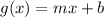
m is slope.

Given slope is 5, we can write:

`g(x)=5x+b`

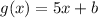
Now,

Given g(k) = 3, we can write:

`\begin{gathered} g(x)=5x+b \\ 3=5k+b \end{gathered}`

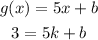
Again, given

g(5) = 2k, so we can write:

`\begin{gathered} g(x)=5x+b \\ 2k=5(5)+b \\ 2k=25+b \end{gathered}`

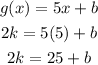
We have two equations is k and b. We can write both in terms of k and solve. Shown below:

Equation 1:

`\begin{gathered} 3=5k+b \\ b=3-5k \end{gathered}`

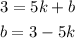
Equation 2:

`b=2k-25`

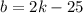
Now, we equate both of these equations and solve for k. Shown below:

`\begin{gathered} 3-5k=2k-25 \\ 3+25=2k+5k \\ 28=7k \\ k=(28)/(7) \\ k=4 \end{gathered}`

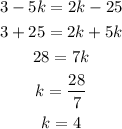
So, the value of k is 4.

k = 4 (answer)