Question

Directions: Write the system of equations that could be used to solve this problem. Then solve the system YOU MUST show the algebraic work (substitution or elimination) that leads to the answer. You may NOT guess and check. 3) Billy's Restaurant ordered 200 flowers for Mother's Doy. They ordered carnations of $1.50 each roses at $5.75 eoch, and daisies of $2.60 each. They ordered mostly comotions, and 20 fewer roses than doisies. The total order came to $589.50. How many of each type of flower was ordered?

Answer 1

daisiesThere are 3 types of flowers.

Let C denote carnations, R denotes roses and D denote daisies.

Billy's Restaurant ordered 200 flowers for Mother's Day.

Mathematically,

`C+R+D=200\text{ eq. 1}`

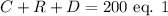
They ordered carnations of $1.50 each, roses at $5.75 each, and daisies of $2.60 each.

The total order came to $589.50.

Mathematically,

`1.50C+5.75R+2.60D=589.50\text{ eq. 2}`

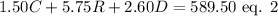
They ordered mostly carnations, and 20 fewer roses than daisies.

Mathematically,

`R=D-20\text{ eq. 3}`

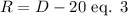
So, we have 3 equations and 3 unknowns.

Let us substitute eq. 3 into eq. 1

`\begin{gathered} C+(D-20)+D=200 \\ C+D-20+D=200 \\ C+2D=200+20 \\ C+2D=220\text{ eq. 4} \end{gathered}`

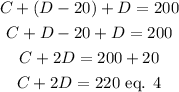
Let us substitute eq. 3 into eq. 2

`\begin{gathered} 1.50C+5.75(D-20)+2.60D=589.50 \\ 1.50C+5.75D-115+2.60D=589.50 \\ 1.50C+8.35D=589.50+115 \\ 1.50C+8.35D=704.5\text{ eq. 5} \end{gathered}`

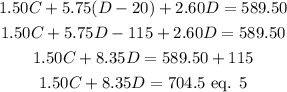
So, now we have eq. 4 and eq. 5 with 2 unknowns. Let's solve them by substitution method.

Separate the variable C in eq. 4

`C=220-2D`

Now substitute it into eq. 5.

`\begin{gathered} 1.50(220-2D)+8.35D=704.5 \\ 330-3D+8.35D=704.5 \\ 330+5.35D=704.5 \\ 5.35D=704.5-330 \\ 5.35D=374.5 \\ D=(374.5)/(5.35) \\ D=70 \end{gathered}`

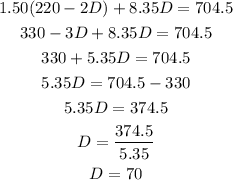
So. we got the number of Daisies that is 70.

Now substitute D = 70 into the previous equation.

`\begin{gathered} C=220-2D \\ C=220-2(70) \\ C=220-140 \\ C=80 \end{gathered}`

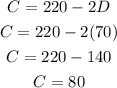
So. we got the number of Carnations that is 80.

Finally, from eq. 3 we get

`\begin{gathered} R=D-20 \\ R=70-20 \\ R=50 \end{gathered}`

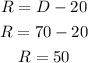
So. we got the number of Roses that is 50.

Therefore.

Number of Carnations = 80

Number of Daisies = 70

Number of Roses = 50

Verification:

Total number of flowers should sum to 200.

80 + 70 + 50 = 200

200 = 200

Hence, we got the correct results.