The above diagram represents the situtation.
The area of the whole lawn is:
200x40 = 8000 sq ft
If 78.75% of the lawn was mowed, then 21.25% ( = 100% - 78.75%) was not mowed. This area is:
8000x21.25% = 1700 sq ft
With the help of the diagram, this area is computed as follows:
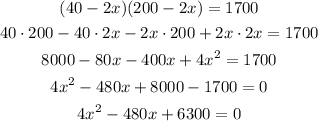
We can solve this equation with the help of the quadratic formula, as follows:
![\begin{gathered} x_(1,2)=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ x_(1,2)=\frac{480\pm\sqrt[]{(-480)^2-4\cdot4\cdot6300}}{2\cdot4} \\ x_(1,2)=\frac{480\pm\sqrt[]{129600}}{8} \\ x_1=(480+360)/(8)=105 \\ x_2=(480-360)/(8)=15 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/6p7uffpvd0c5hg9p0srzh5xralj3fdo9ou.png)
The first solution, x = 105 ft, has no sense in the context of the problem. It would be longer than the width of the rectangular lawn. In consequence, the correct answer is x = 15 ft.
The width of the mowed strip is 15 ft