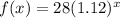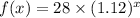
The percent change is 12%, meaning after each interval x the new value is 112% times the previous value. This can be expressed as (for x = 1)
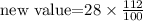
when x = 2 the above value becomes the "previous value" and therefore, the new value will be
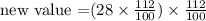
when the above becomes the previous value the new value then will be
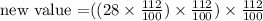
and so on until we have x number of 122/100 =1.12 terms. Then the new value for any x can be written as
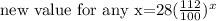
or