Question

1 A football kicked at ground level with an initial velocity of 64 fret per second.standard fox - 641IV. GraphI.vertex form: --10-27 - 14intercept formy - 4)a. To find the maximum height of the football.Form: ChooseExplana1 II III IVb. To find the begle afer scoadsForm: (C)EmplaceI II III IV.. To find the time when the ball hits the groundForm (case)ExplI II III IVd. To find an estimate of the time when the football is 40 feetchForm Goose ExplI II III IV

Answer 1

a) Form I - Since the coefficients a, b and c are explicitly displayed.

We've used the Vertex Formula and the Y-coordinate for the height. 64 ft.

b) 48 ft. The Vertex form was picked as a matter of convenience since we had only to plug into t=3).

c) The Intercept form. t_2 = 4. This form was chosen since it displays the root(s) in a factored form, so we don't need to use the Quadratic Formula to find out the roots.

d) The intercept form. it is more convenient to work with lesser degrees than using the vertex form. t≈ 3.2 and t≈ 0.8 (rounded off to nearest tenth)

a) Let's start by finding the maximum height, i.e. the y-coordinate at the Vertex of that parabola. y = -16t²+64t

Form I - Standard Form

`\begin{gathered} V=(h,k)\Rightarrow V=((-b)/(2a),(-\Delta)/(4a)) \\ Y_v=(-(64^2-4(-16)(0))/(4(-16))=64 \end{gathered}`

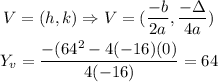
We pick the standard form because the coefficients are explicitly displayed what makes it easier than expand the parentheses.

0. Note that we've used the formula for the Vertex, and since the y-axis indicates the height while the x-axis the time, we need the y-coordinate, in this case: ,64 ft

,

1. Note also that we only need to pick one form. In this case, the standard form.

,

2. The Y-coordinate is 64 because when x=-2 (the x-coordinate) is plugged into that equation that yields 64. Hence the Vertex of that Parabola is at point (-2,64)

b) The height after 3 seconds is found when we plug into the variable t = 3

So choosing the Vertex form (we could have chosen for this question any of them):

Vertex Form (II)

`\begin{gathered} y=-16(t-2)^2+64 \\ y=-16(3-2)^2+64 \\ y=-16(1)^2+64 \\ y=-16+64 \\ y=48 \end{gathered}`

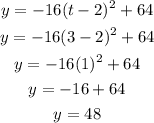
Therefore, after 3 seconds that football is 48 feet in height.

c) To find the time when the ball hits the ground is to find one of those roots

≠0 since the parabola passes through the origin (0,0)

Examining the forms, let's pick the intercept form since it's already factored and then it's easier to find out the roots without using the Quadratic formula:

Form III - Intercept form

`\begin{gathered} y=-16t(t-4) \\ -16t(t-4)=0 \\ t_1=0 \\ t-4=0 \\ t_2=4 \end{gathered}`

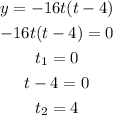
Since it's already factored we can pick one factor and then equate to zero and then we find the other root. The first root is 0 and the second one is 4.

So the ball hits the ground 4 seconds after being kicked off.

d) To find out the estimate (an approximation) of the time when the ball is 40 feet high we need to plug into one of those equation forms y =40. So let's do it let's pick for that the Intercept form too:

`\begin{gathered} y=-16t(t-4) \\ 40=-16t(t-4) \\ (40)/(-16)=(-16t(t-4))/(-16) \\ -2.5=t(t-4) \\ -2.5=t^2-4t \\ 0=t^2-4t+2.5 \\ t^2-4t+2.5=0 \\ t=\frac{4\pm\sqrt[]{6}}{2} \\ t_1=\frac{4+\sqrt[]{6}}{2}\approx3.2 \\ t_2=\frac{4-\sqrt[]{6}}{2}\approx0.8 \end{gathered}`

So the ball will be 40 high in approximately 3.2 seconds and 0.77 (approximately 0.8 seconds)

3) Hence the answers are:

a) Form I - Since the coefficients a, b and c are explicitly displayed.

We've used the Vertex Formula and the Y-coordinate for the height. 64 ft.

b) 48 ft. The Vertex form was picked as a matter of convenience since we had only to plug into t=3).

c) The Intercept form. t_2 = 4. This form was chosen since it displays the root(s) in a factored form, so we don't need to use the Quadratic Formula to find out the roots.

d) The intercept form. it is more convenient to work with lesser degrees than using the vertex form. t≈ 3.2 and t≈ 0.8 (rounded off to nearest tenth)