Question

Assume that adults have IQ scores that are normally distributed with a moon of 101 and a standard deviation of 20.4. Find the probability that a randomly selectedadult has an IQ greater than 131.9. (Hint: Draw a graph.)The probability that a randomly selected adult from this group has an IQ greater than 131.9 in(Round to four decimal places as needed)correct

Answer 1

The graph of this distribution is:

Now, from it we know that the probability has to be less 0.1586 but more than 0.0227.

To find the probability we have to use the z-score to transform our distribution to a standard normal distribution.

The z-score is given by:

`z=(x-\mu)/(\sigma)`

Then in this case we have:

`\begin{gathered} z=(131.9-101)/(20.4) \\ z=1.5147 \end{gathered}`

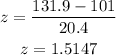
Then our probability is:

`P(X>131.9)=P(Z>1.5147)`

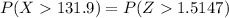
Looking on a table for the value of the probability we have that:

`P(X>131.9)=P(Z>1.5147)=0.0649`

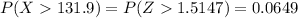
Therefore the probability is 0.0649; which is the same as 6.49%.