ANSWER:
a. 0.4207
b. 0.2578
c. 0.5468
Explanation:
Given:
μ = 85
σ = 20
Now, the probabilities are obtained, after obtaining the z-score for the given corresponding sample data points. We calculate the value of z as follows:

We calculate for each case:
a. P( x > 89)
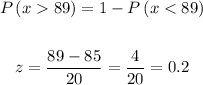
We locate this value in the normal table:
Therefore:
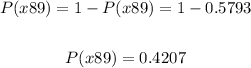
b. P (x < 72)
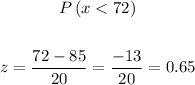
We locate this value in the normal table:
Therefore:
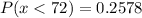
c. P (70 < x < 100)
![\begin{gathered} P(70We locate this value in the normal table:<p>Therefore:</p>[tex]\begin{gathered} P(70\lt x\lt100)= P(x\lt100)- P(x\lt70) \\ \\ P(70\lt x\lt100)=0.7734-0.2266 \\ \\ P(70\lt x\lt100)=0.5468 \end{gathered}]()