Question

A Septa bus is approaching an underpass at 13.00 m/s. The top of the bus is 3.50 meters high. A physics student is on the top of the bridge 7.00 meters above the road the bus is on. She throws a snowball horizontally in the direction of the oncoming bus. She lets go of the snowball 1.40 meters above the bridge when the bus is 25.00 meters from the bridge. If thebus is 12.00 meters long, what range of velocities can she throw the snowball and have it landon the bus?

Answer 1

First let's calculate the total falling time of the snowball.

It will fall from the height of 8.4 meters (7 m from the bridge plus 1.4 m from the student) to the height of 3.5 meters (top of the bus), so the total height is 4.9 meters.

Calculating the falling time, we have:

`\begin{gathered} h=(gt^2)/(2) \\ 4.9=(9.8t^2)/(2) \\ 4.9=4.9t^2 \\ t=1\text{ s} \end{gathered}`

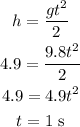
After 1 second, the bus will move 13 meters, so it will be 12 meters from the bridge when the snowball is in the desired height.

The bus has 12 meters long, so the range of horizontal distance the snowball needs to travel is from 12 meters to 24 meters:

Since the travel time of the snowball is 1 second, the minimum and maximum speed the snowball should be thrown is:

`\begin{gathered} d_(\min )=v_(\min )\cdot t \\ 12=v_(\min )\cdot1 \\ v_(\min )=12\text{ m/s} \\ \\ d_(\max )=v_(\max )\cdot t \\ 24=v_(\max )\cdot1 \\ v_(\max )=24\text{ m/s} \end{gathered}`

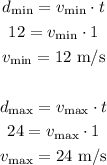
Therefore the range of velocities is from 12 m/s to 24 m/s.