Question

I don't understand how to explain what they are question : which statement explains how the lines x-y=2 and y=x+1 are related?

Answer 1

The general line equation in slope-intercept form is

`y=mx+b`

where m is the slope and b is the y-intercept.

- Now, two lines are parallel if they have the same slope

- Two lines are perpendicular if

`M=-(1)/(m)`

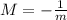
where M is the slope of the other line.

In our case, we must see how the slopes are related. In the first case, we have

`y=x-2`

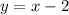
in the second case, we have

`y=x+1`

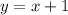
since the slope is the coefficient of the variable x, we can note that both lines have slope equal 1. This means that the lines are parellel.