Question

Solve for yLog 5 + log y = log 40

Answer 1

y = 8

Step-by-step explanation

To solve this equation, first, we have to apply the product property of logarithms,

`\log(ab)=\log a+\log b`

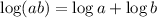
In this equation we have the right side of the property written above, so applying this rule we have,

`\begin{gathered} \log5+\log y=\log40 \\ \\ \log(5y)=\log40 \end{gathered}`

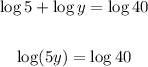
If two logarithms have the same base and are equal, then their arguments are equal,

`5y=40`

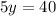
Finally, divide both sides by 5,

`\begin{gathered} (5y)/(5)=(40)/(5) \\ \\ y=8 \end{gathered}`

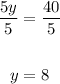
Hence, the solution is y = 8.