Step 1:
To select or choose 5 students out of 21 students involve combination.
In mathematics, a combination is a selection of items from a collection, such that the order of selection does not matter.
Step 2:
Use the formula below to find the number of ways 5 students can be selected from 21 students.
n = 21 and r = 5
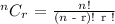
Step 3:
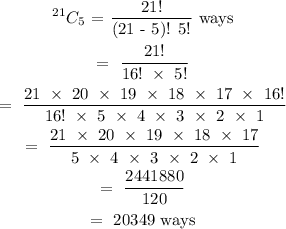
Final answer