Question

The president of the college asked a fraternity to submit a list of 5 students to serve as guides at a school function. They have 21 students who are available to help. In how many ways can the students be chosen?

Answer 1

Step 1:

To select or choose 5 students out of 21 students involve combination.

In mathematics, a combination is a selection of items from a collection, such that the order of selection does not matter.

Step 2:

Use the formula below to find the number of ways 5 students can be selected from 21 students.

n = 21 and r = 5

`^nC_r\text{ = }\frac{n!}{(n\text{ - r)! r !}}`

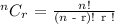
Step 3:

`\begin{gathered} ^(21)C_5\text{ = }\frac{21!}{(21\text{ - 5)! 5!}}\text{ ways} \\ =\text{ }\frac{21!}{16!\text{ }*\text{ 5!}} \\ =\text{ }\frac{21\text{ }*\text{ 20 }*\text{ 19 }*\text{ 18 }*\text{ 17 }*\text{ 16!}}{16!\text{ }*\text{ 5 }*\text{ 4 }*\text{ 3 }*\text{ 2 }*\text{ 1}} \\ =\text{ }\frac{21\text{ }*\text{ 20 }*\text{ 19 }*\text{ 18 }*\text{ 17}}{5\text{ }*\text{ 4 }*\text{ 3 }*\text{ 2 }*\text{ 1}} \\ =\text{ }(2441880)/(120) \\ =\text{ 20349 ways} \end{gathered}`

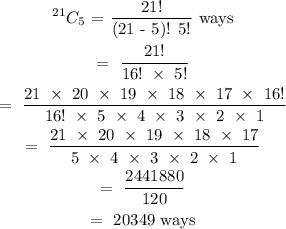
Final answer