the coordinate of B is (4,0)
and D is (8, 10)
the coordinate of C is (4,5) and D is (8, 10)
so the equation of the line passing through two-point is given as follows,
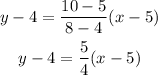
for point (16, 20)
substitute the value of x and y in the above expression

so it is not satisfying the equation of the line that means the point does not lie on this line