The sides of a triangle measure 4,6, and 7. If the shortest side of a similar triangle is 12, what is the perimeter of the larger triangle?

Question

asked Sep 9, 2023 206k views

1 Answer

Scarface · Answer 1 · 2023-09-13T18:14:42+0000

Given that both triangles are similar, then their corresponding sides satisfy a proportion.

The next relation must be satisfied:

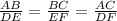
Let's suppose that AB and DE are the shortest sides of each triangle, then:

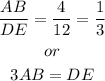
$\begin{gathered} (AB)/(DE)=(4)/(12)=(1)/(3) \\ or \\ 3AB=DE \end{gathered}$

Also,

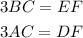
$\begin{gathered} 3BC=EF \\ 3AC=DF \end{gathered}$

The perimeter of the smaller triangle is,

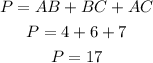
$\begin{gathered} P=AB+BC+AC \\ P=4+6+7 \\ P=17 \end{gathered}$

The perimeter of the larger triangle is,

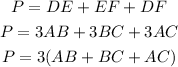
$\begin{gathered} P=DE+EF+DF \\ P=3AB+3BC+3AC \\ P=3(AB+BC+AC) \end{gathered}$

But, AB + BC + AC is the perimeter of the smaller triangle, which is 17, then the perimeter of the larger triangle is 3*17 = 51