For the ratio test of a series the ratio is defined as:
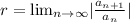
And we have three possible outcomes:
- r<1 and the series converges.
- r>1 and the series diverges.
- r=1 and the test is inconclusive.
Knowing this let's apply the test to the series given by the question. We have:
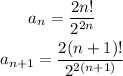
As you can see both expressions are always positive so when writing the ratio we don't need to add the absolute value symbols. Then the ratio is:

Here is important to remember a property of the factorial:
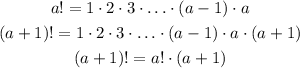
And a property of powers:
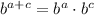
Using these properties we get:
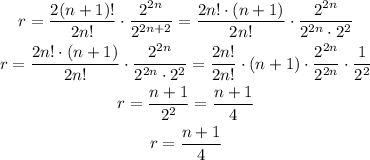
So the answer to part (a) is:
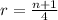
For part (b) we have:
The ratio depends on n. As n increases the ratio increases and gets greater than 1:
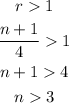
So for any n>3 the ratio is greater than 1 which means that this value of r tells us that the series diverges.