Question

I need help with this practice problem This problem asks two things, (a) and (b), answer these as they go along with the problem

Answer 1

For the ratio test of a series the ratio is defined as:

`r=\lim _(n\to\infty)\lvert(a_(n+1))/(a_n)\rvert`

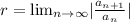
And we have three possible outcomes:

- r<1 and the series converges.

- r>1 and the series diverges.

- r=1 and the test is inconclusive.

Knowing this let's apply the test to the series given by the question. We have:

`\begin{gathered} a_n=(2n!)/(2^(2n)) \\ a_(n+1)=(2(n+1)!)/(2^(2(n+1))) \end{gathered}`

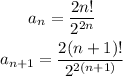
As you can see both expressions are always positive so when writing the ratio we don't need to add the absolute value symbols. Then the ratio is:

`\begin{gathered} r=(a_(n+1))/(a_n)=((2(n+1)!)/(2^(2(n+1))))/((2n!)/(2^(2n)))=(2(n+1)!)/(2^(2(n+1)))\cdot(2^(2n))/(2n!) \\ r=(2(n+1)!)/(2n!)\cdot(2^(2n))/(2^(2n+2)) \end{gathered}`

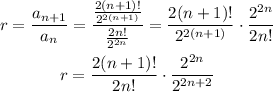
Here is important to remember a property of the factorial:

`\begin{gathered} a!=1\cdot2\cdot3\cdot\ldots\cdot(a-1)\cdot a \\ (a+1)!=1\cdot2\cdot3\cdot\ldots\cdot(a-1)\cdot a\cdot(a+1) \\ (a+1)!=a!\cdot(a+1) \end{gathered}`

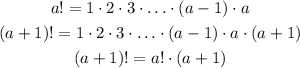
And a property of powers:

`b^(a+c)=b^a\cdot b^c`

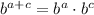
Using these properties we get:

`\begin{gathered} r=(2(n+1)!)/(2n!)\cdot(2^(2n))/(2^(2n+2))=(2n!\cdot(n+1))/(2n!)\cdot(2^(2n))/(2^(2n)\cdot2^2) \\ r=(2n!\cdot(n+1))/(2n!)\cdot(2^(2n))/(2^(2n)\cdot2^2)=(2n!)/(2n!)\cdot(n+1)\cdot(2^(2n))/(2^(2n))\cdot(1)/(2^2) \\ r=(n+1)/(2^2)=(n+1)/(4) \\ r=(n+1)/(4) \end{gathered}`

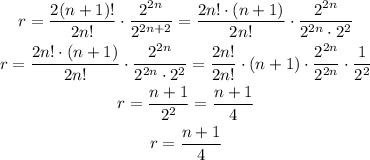
So the answer to part (a) is:

`r=(n+1)/(4)`

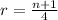
For part (b) we have:

The ratio depends on n. As n increases the ratio increases and gets greater than 1:

`\begin{gathered} r>1 \\ (n+1)/(4)>1 \\ n+1>4 \\ n>3 \end{gathered}`

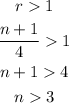
So for any n>3 the ratio is greater than 1 which means that this value of r tells us that the series diverges.