We must solve, using the linear combination method, the following system of equations:
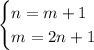
(1) We reorder the variables in the equations such that the variables are ordered in columns
We rewrite the first equation in the following way:
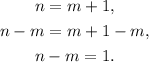
We rewrite the second equation in the following way:
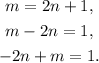
So, our system of equation is equivalent to:

2) We solve for n
Summing both equations, we get:
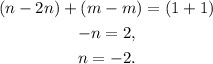
NOTE: When we sum the equations:
0. we sum the left side of eq. 1 with the left side of eq. 2,
,
1. we sum the right side of eq. 1 with the right side of eq. 2,
3) We solve for m
We multiply the first equation by 2:

Summing both equations, we get:
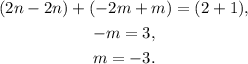
Answer
The solution of the system of equations is:
