To solve the exercise you can use this property of the absolute value:
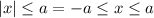
So, in this case, you have
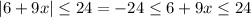
Then
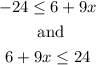
To solve the first part you can proceed like this:
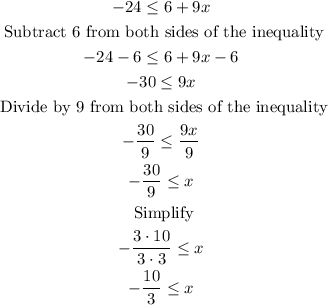
To solve the second part you can proceed like this:

Therefore, the solution to the inequality will be
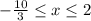
Graphically