In a parallelogram the opposite angles are equal in measure, then, in our case:
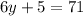
Solving for y:
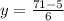
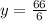
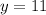
Also, we have to consider that any two adjacent angles add up to 180°, meaning:
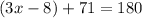
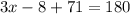
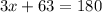
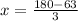
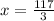
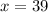
Using the same logic as the one used to calculate y, we can do the following:
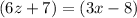
However, as we know x = 39° we can solve for z:
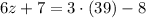
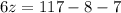
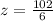
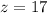
Answer:
• x = 39°
,
• y = 11°
,
• z = 17°