Explanation
Given:
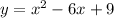
Required: We are required to determine the discriminant of the given equation and the nature of its roots.
This is achieved thus:
We know that the formula for discriminant is given as:
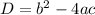
We also know we can determine the nature of the roots thus:

Therefore, we have:

Hence, the answer is:
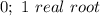
The last option is correct.