Question

Find the discriminant of y=x^2-6x+9 and describe the nature of the roots.

Answer 1

Explanation

Given:

`y=x^2-6x+9`

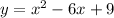
Required: We are required to determine the discriminant of the given equation and the nature of its roots.

This is achieved thus:

We know that the formula for discriminant is given as:

`D=b^2-4ac`

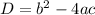
We also know we can determine the nature of the roots thus:

`\begin{gathered} (a)\text{ }D>0\text{ \lparen two distinct real roots\rparen } \\ (b)\text{ }D=0\text{ \lparen only one real root\rparen} \\ (c)\text{ }D<0\text{ \lparen two distinct complex roots\rparen} \end{gathered}`

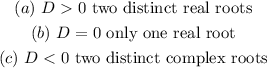
Therefore, we have:

`\begin{gathered} y=x^(2)-6x+9 \\ where \\ a=1,b=-6,c=9 \\ \\ \therefore D=b^2-4ac \\ D=(-6)^2-4\cdot1\cdot9 \\ D=36-36 \\ D=0 \end{gathered}`

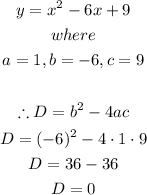
Hence, the answer is:

`0;\text{ }1\text{ }real\text{ }root`

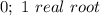
The last option is correct.