The points of inflection of a function are given by the zeros of the second derivative. The first derivative of our function is:
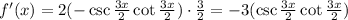
Using the product rule, the second derivative of our function is:
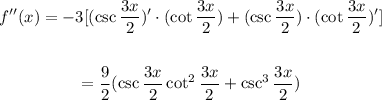
Then, the zeros of the second derivative are the solutions for the following equation:
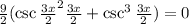
Simplifying this expression, we have:
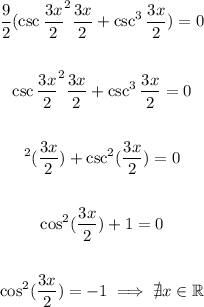
Our function has no inflection points.