Question

I need to determine which system of equations it is a solution too if any

Answer 1

To solve this exercise you have to solve each system of equations.

a)

`\begin{cases}y=4x-5 \\ y=-6x+25\end{cases}`

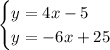
To solve this equation system you have to equal both equations and solve for x:

`4x-5=-6x+25`

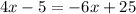
- Pass -6x to the left side of the equation by applying the opposite operation to both sides of it

`\begin{gathered} 4x+6x-5=-6x-6x+25 \\ 10x-5=25 \end{gathered}`

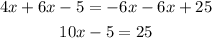
- Add 5 to both sides of the equal sign:

`\begin{gathered} 10x-5+5=25+5 \\ 10x=30 \end{gathered}`

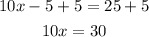
- Divide both sides by 10

`\begin{gathered} (10x)/(10)=(30)/(10) \\ x=3 \end{gathered}`

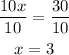
- Replace the value of x in one of the equations and solve for y:

`\begin{gathered} y=4x-5 \\ y=4\cdot3-5 \\ y=12-5 \\ y=7 \end{gathered}`

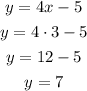
The solution for this equation system is (3,7)

b)

`\begin{cases}2y=10x-12 \\ y=-7x+42\end{cases}`

Replace the second equation into the first one:

`\begin{gathered} 2y=10x-12 \\ 2(-7x+42)=10x-12 \end{gathered}`

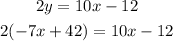
- Distribute the multiplication on the parentheses term:

`\begin{gathered} 2\cdot(-7x)+2\cdot42=10x-12 \\ -14x+84=10x-12 \end{gathered}`

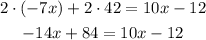
-Subtract 10x to both sides of the expression:

`\begin{gathered} -14x-10x+84=10x-10x-12 \\ -24x+84=-12 \end{gathered}`

-Subtract 84 to both sides of the equal sign:

`\begin{gathered} -24x+84-84=-12-84 \\ -24x=-96 \end{gathered}`

-Divide both sides by -24

`\begin{gathered} (-24x)/(-24)=(-96)/(-24) \\ x=4 \end{gathered}`

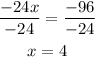
- Replace the value of x in the second equation and solve for y:

`\begin{gathered} y=-7x+42 \\ y=-7\cdot4+42 \\ y=-28+42 \\ y=14 \end{gathered}`

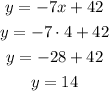
The solution for this equation system is (4,14)

c)

`\begin{cases}3y-9x=-21 \\ y+12x=23\end{cases}`

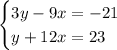
- Write the second equation for y:

`\begin{gathered} y+12x=23 \\ y+12x-12x=23-12x \\ y=-12x+23 \end{gathered}`

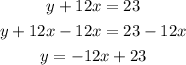
- Replace the expression in the first equation

`\begin{gathered} 3y+9x=-21 \\ 3(-12x+23)+9x=-21 \end{gathered}`

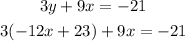
-Distribute the multiplication on the parentheses term

`\begin{gathered} 3\cdot(-12x)+3\cdot23-9x=-21 \\ -36x+96-9x=-21 \\ -36x-9x+69=-21 \\ -45x+69=-21 \end{gathered}`

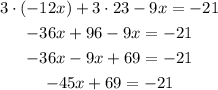
- Subtract 69 to both sides of the equal sign

`\begin{gathered} -45x+69-69=-21-69 \\ -45x=-90 \end{gathered}`

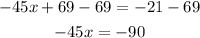
-Divide both sides by -45

`\begin{gathered} (-45x)/(-45)=(-90)/(-45) \\ x=2 \end{gathered}`

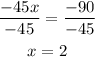
-Replace the value of x in the expression obtained for y and solve:

`\begin{gathered} y=-12x+23 \\ y=-12\cdot2+23 \\ y=-24+23 \\ y=-1 \end{gathered}`

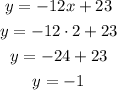
The solution of this equation system is (2,-1)

d)

`\begin{cases}2y-21x=-24 \\ 2y+8x=52\end{cases}`

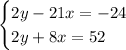
- Write the second equation for y:

`\begin{gathered} 2y+8x=52 \\ 2y+8x-8x=52-8x \\ 2y=52-8x \\ (2y)/(2)=(52)/(2)-(8x)/(2) \\ y=-4x+26 \end{gathered}`

-Replace the expression in the first equation:

`\begin{gathered} 2y-21x=-24 \\ 2(-4x+26)-21x=-24 \end{gathered}`

-Distribute the multiplication on the parentheses term:

`\begin{gathered} 2*\mleft(-4x\mright)+2*26-21x=-24 \\ -8x+52-21x=-24 \\ -8x-21x+52=-24 \\ -29x+52=-24 \end{gathered}`

-Subtract 52 to both sides of the equation:

`\begin{gathered} -29x+52-52=-24-52 \\ -29x=-76 \end{gathered}`

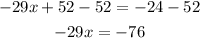
-Divide both sides by -29

`\begin{gathered} (-29x)/(-29)=(-76)/(-29) \\ x=(76)/(29) \end{gathered}`

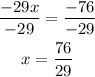
-Replace this value in the expression obtained for y:

`\begin{gathered} y=-4x+26 \\ y=-4\cdot(76)/(29)+26 \\ y=-(304)/(29)+26 \\ y=(450)/(29) \end{gathered}`

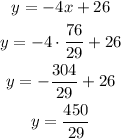
The solution to this equation system is (76/29,450/29)

The answer for this exercise is:

a → (3,7)

c → (2,-1)

b → (4,14)

e → (4,20)