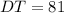For this exercise you need to remember the Intersecting chords theorem. This states that the product of the lengths of the segments of one chord is equal to the product of the lengths of the segments of the other chord.
In this case you can set up that:
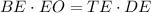
You can identify that:

Then, since you don't know the length TE, you can substitute these values into the equation and solve for TE:
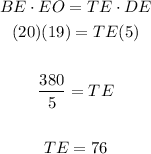
As you can observe, the length DT can be found by adding the length TE and the length DE. Then:
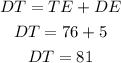
The answer is: