Question

Consider the angle shown below with an initial ray pointing in the 3-o'clock direction that measures θ radians (where 0≤θ<2π). The circle's radius is 2.3 units long and the terminal point is (−1.06,2.04).What is the slope of the terminal ray?m=Then, tan−1(m)=Does the number we get in part (b) give us the correct value of θ? ? Therefore, θ=

Answer 1

m = -1.92

tan^-1(m) = -1.09 rad

-1.09 is an incorrect value for θ

θ = 2.05 rad

Step-by-step explanation:

If the terminal point of a ray that starts in the origin has the coordinates (x, y), we can calculate the slope of the ray as:

`m=(y)/(x)`

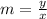
Therefore, the slope of the terminal ray with terminal point (-1.06, 2.04) is:

`m=(2.04)/(-1.06)=-1.92`

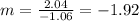
Then, using the calculator, we get that the inverse function of the tangent is equal to:

`\tan ^(-1)(-1.92)=-1.09\text{ rad}`

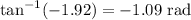
-1.09 rad is a negative number, so it is an incorrect value of θ. This equation calculated the supplement of θ, so the correct value of θ is:

`\theta=\pi\text{ rad - 1.09 rad = 2.05 rad}`

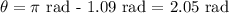
Therefore, the answers are:

m = -1.92

tan^-1(m) = -1.09 rad

-1.09 is an incorrect value for θ

θ = 2.05 rad