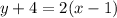The slope-intercept form of an equation of the line is:

Where m is known as the slope and b as the y-intercept. We are being told that the y-intercept is -6 so we already have b=-6.
We still need to find the slope. In order to find it we can use the information about the x-intercept. The x-intercept is the x value that meets:
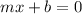
We know that the x-intercept is so we have an equation for m (we also use the fact that b=-6):

We add 6 at both sides of the equation:
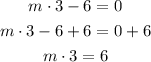
And we divide both sides by 3:
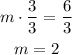
Now that we found the slope we can write the complete equation of the line:
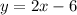
Which means that the answer is the second option.
The slope-point form of an equation of the line is:
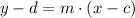
Where m is the slope and (c,d) is a point through which the line passes.
We already know the slope, it's m=2 so we have:
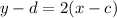
We need a point (c,d). If the line passes through that point then taking x=c and y=d is a solution to the equation in the slope-intercept form:
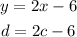
If we take a random value for c, for example c=1 we get:
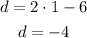
So we know the line passes through point (c,d)=(1,-4). Then the point-slope form can be written as: