Question

Which expressions are equivalent to the one below? Check all that apply. 9X O A. (3:3) * O B. 3x. 3x c. 32.31 O D. 3.32% O E. 3. 34 F. 32x

Answer 1

Given:

`9^x\text{ is the given expression.}`

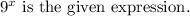
Required:

To find the equivalent expressions from the given options.

Step-by-step explanation:

We have to simplify all the expressions and know which expressions are equal to the given expression.

`\begin{gathered} (3\cdot3)^x=9^x \\ 3^x\cdot3^x=3^(2x)=(3^2)^x=9^x \\ 3^2\cdot3^x=3^(2+x) \\ 3\cdot3^(2x)=3^(1+2x) \\ 3\cdot3^x=3^(1+x) \\ 3^(2x)=(3^2)^x=9^x \end{gathered}`

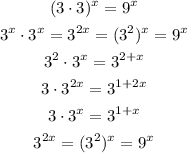
Expressions equivalent to the given expression are,

`(3\cdot3)^x,\text{ }3^x\cdot3^x,\text{ }3^(2x)`

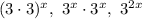
Final Answer:

`(3\cdot3)^x,(\text{3})^x\cdot3^x,(\text{3})^(2x)`

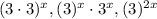
Options A,B and F are the correct answers.