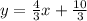Answer:
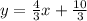
Given:
A (5, 10)
B (-13, -14)
First, let us find the slope


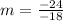
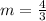
Next, we will use the following formula to solve for the equation of the line

Using the point A (5, 10), and the slope, solve for b
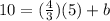
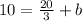
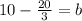
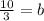
Now that we have the slope m, and the value of b, substitute it to this equation to get the equation of the line