Question

I need the answer to this at least 3 decimal points

Answer 1

The sum of angles of any triangle is 180 degrees

From the given figure

Since mSince m

Then subtract them from 180 degrees to find m
`\begin{gathered} m\angle B=180-90-53 \\ m\angle B=\mathring{37} \end{gathered}`

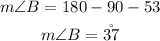
The measure of angle B is 37 degrees

By using the trigonometry ratios we can find the lengths of AB and BC

Since the opposite side of Since the adjacent side of

We can use the tan C to find AB

`\begin{gathered} \tan C=\frac{opp.}{\text{adj.}} \\ \tan C=(AB)/(AC) \end{gathered}`

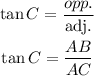
Since Since AC = 13

`\tan 53=(AB)/(13)`

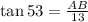
By using cross multiplication

`\begin{gathered} AB=13*\tan 53 \\ AB=17.25158268 \end{gathered}`

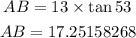
Round it to 3 decimal places, then

AB = 17.252

Since BC is the hypotenuse of the triangle, then

We can use the cos ratio to find it

Since cos = adjacent/hypotenuse, then

`\begin{gathered} \cos C=(AC)/(BC) \\ \cos 53=(13)/(BC) \end{gathered}`

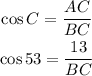
By using the cross multiplication

`BC*\cos 53=13`

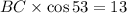
Divide both sides by cos 53

`\begin{gathered} BC=(13)/(\cos 53) \\ BC=21.60132183 \end{gathered}`

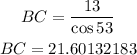
Round it to 3 decimal places, then

BC = 21.601