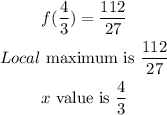Question

Find the open intervals where the function is increasing and the intervals where the function is decreasing. Determine the relative extreme of the function. F(x)=x^3-5x^2+8x

Answer 1

We are given the function

`f(x)=x^3-5x^2+8x`

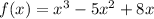
First, we will find the critical point. To find the critical points, we set f'(x) = 0

`\begin{gathered} f(x)=x^(3)-5x^(2)+8x \\ By\text{ differentiating} \\ f^(\prime)(x)=3x^2-10x+8 \end{gathered}`

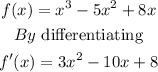
Now, we set f'(x) = 0

`\begin{gathered} f^(\prime)(x)=3x^(2)-10x+8 \\ 3x^2-10x+8=0 \\ (3x-4)(x-2)=0 \\ x=2,(4)/(3) \end{gathered}`

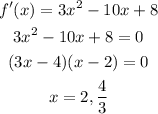
So we have to split the interval into

`(-\infty,(4)/(3)),((4)/(3),2),(2,\infty)`

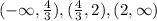
We check the intervals

`\begin{gathered} On\text{ the interval }(-\infty,(4)/(3)) \\ f^(\prime)(x)\text{ is always positive} \\ Therefore,\text{ f is increasing on this interval} \end{gathered}`

The next interval

`\begin{gathered} On\text{ the interval }((4)/(3),2) \\ f^(\prime)(x)\text{ is negative on this interval} \\ Therefore,\text{ f is decreasing on the interval} \end{gathered}`

The last interval

`\begin{gathered} On\text{ the interval }(2,\infty) \\ f^(\prime)(x)\text{ is positive on this interval} \\ Therefore,\text{ f is increasing on the interval} \end{gathered}`

The graph of the function is given below

The function is increasing on the interval

`(-\infty,(4)/(3))\cup(2,\infty)`

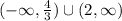
The function is decreasing on the interval

`((4)/(3),2)`

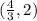
Local Minimum

`\begin{gathered} f(2)=4 \\ Local\text{ minimum is 4} \\ x\text{ value is 2} \end{gathered}`

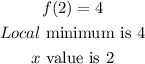
Local Maximum

`\begin{gathered} f((4)/(3))=(112)/(27) \\ Local\text{ maximum is }(112)/(27) \\ x\text{ value is }(4)/(3) \end{gathered}`