Solution
Step 1:
Define the variables:
s = sugar cookie dough
g = gingerbread cookie dough
Step 2:
Write systems of equations.
s = cost sugar cookie dough
g = cost gingerbread cookie dough
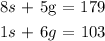
Solve
Use the substitution method to substitute s from the second equation into the first equation.
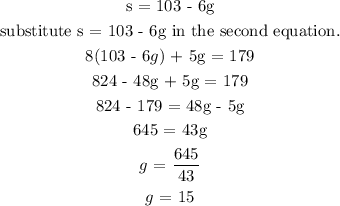
Next, find the value of s.
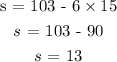
Write the solution as a complete sentence below:
One package of sugar cookie dough cost = $13
One package of gingerbread cookie dough cost = $15